Izračuni magnetnih vezij

V električnih strojih in aparatih je magnetni tok F koncentriran v magnetnem krogu (feromagnetnem jedru) in zračnih režah tega magnetnega kroga. To pot magnetnega pretoka imenujemo magnetni krog.

Magnetno vezje je kot električno vezje. Magnetni pretok Ф je podoben električnemu toku I, indukcija В je podobna gostoti toka, magnetna sila (ns) Fн (H ∙ l = I ∙ ω) ustreza e. itd. z

V najpreprostejšem primeru ima magnetni tokokrog povsod enak prerez in je izdelan iz homogenega magnetnega materiala. Za določitev n. z l ∙ ω, potrebnim za zagotovitev zahtevane indukcije B, se ustrezna jakost H določi iz krivulje magnetizacije in pomnoži s srednjo dolžino magnetne silnice l: H ∙ l = I ∙ ω = Fm.

Od tu se določi zahtevani tok I ali število ovojev ω tuljave.

Kompleksno magnetno vezje ima običajno odseke z različnimi odseki in magnetnimi materiali. Ti odseki so običajno zaporedno povezani, zato skozi vsakega od njih poteka isti magnetni tok F.Indukcija B v vsakem prerezu je odvisna od preseka odseka in se izračuna za vsak prerez posebej po formuli B = Φ∶S.

Za različne vrednosti indukcije se intenzivnost H določi iz krivulje magnetizacije in pomnoži s povprečno dolžino daljnovoda ustreznega odseka vezja. Če povzamemo posamezna dela, dobimo celotno n. c. magnetno vezje:

Fm = I ∙ ω = H1 ∙ l1 + H2 ∙ l2 + H3 ∙ l3 + … ki določa tok magnetiziranja ali število ovojev tuljave.

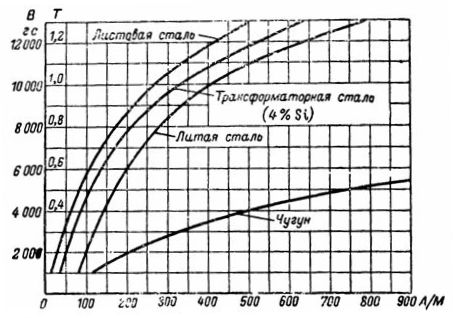
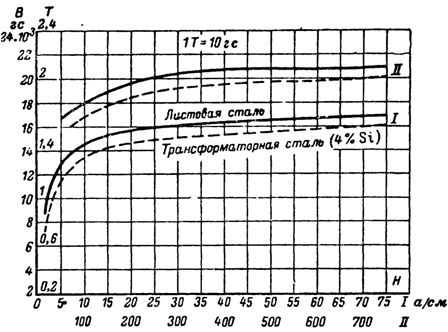
Magnetizacijske krivulje

Primeri za

1. Kolikšen mora biti magnetizacijski tok I tuljave z 200 ovoji, da je n. c) ustvaril v litoželeznem obroču magnetni pretok Ф = 15700 Ms = 0,000157 Wb? Povprečni polmer litoželeznega obroča je r = 5 cm, premer njegovega preseka pa d = 2 cm (slika 1).

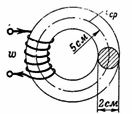
riž. 1.

Odsek magnetnega kroga S = (π ∙ d ^ 2) / 4 = 3,14 cm2.

Indukcija v jedru je: B = Φ∶S = 15700∶3,14 = 5000 G.

V sistemu MKSA je indukcija: B = 0,000157 Wb: 0,0000314 m2 = 0,5 T.

Iz krivulje magnetizacije litega železa najdemo zahtevano jakost H, ki je enaka 750 A / m za B = 5000 G = 0,5 T. Moč magnetiziranja je enaka: I ∙ ω = H ∙ l = 235,5 Av.

Zato je zahtevani tok I = (H ∙ l) / ω = 235,5 / 200 = 1,17 A.

2. Zaprto magnetno vezje (slika 2) je izdelano iz jeklenih plošč transformatorja. Koliko ovojev mora biti v tuljavi s tokom 0,5 A, da ustvari magnetni pretok v jedru Ф = 160000 Ms = 0,0016 Wb?

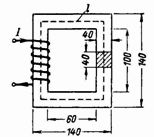
riž. 2.

Prerez jedra S = 4 ∙ 4 = 16 cm2 = 0,0016 m2.

Indukcija jedra B = F / S = 160000/16 = 10000 Gs = 1 T.

Glede na krivuljo magnetizacije transformatorskega jekla najdemo za B = 10.000 Gs = 1 T jakost H = 3,25 A / cm = 325 A / m.

Povprečna dolžina magnetne silnice je l = 2 ∙ (60 + 40) + 2 ∙ (100 + 40) = 480 = 0,48 m.

Magnetna sila Fm = I ∙ ω = H ∙ l = 3,25 ∙ 48 = 315 ∙ 0,48 = 156 Av.

Pri toku 0,5 A je število ovojev ω = 156 / 0,5 = 312.

3. Magnetno vezje, prikazano na sl. 3 je podoben magnetnemu krogu iz prejšnjega primera, le da ima zračno režo δ = 5 mm. Kaj bi moralo biti n. s. in tok tuljave tako, da je magnetni pretok enak kot v prejšnjem primeru, to je F = 160000 Ms = 0,0016 Wb?

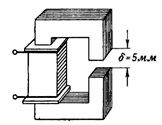
riž. 3.

Magnetno vezje ima dva zaporedno vezana odseka, katerih presek je enak kot v prejšnjem primeru, to je S = 16 cm2. Tudi induktivnost je enaka B = 10000 G = 1 T.

Povprečna dolžina jeklene magnetne črte je nekoliko krajša: lс = 48-0,5 = 47,5 cm ≈0,48 m.

Magnetna napetost v tem odseku magnetnega vezja je Hc ∙ lc = 3,25 ∙ 48≈156 Av.

Poljska jakost v zračni reži je: Hδ = 0,8 ∙ B = 0,8 ∙ 10000 = 8000 A / cm.

Magnetna napetost v prerezu zračne reže Hδ ∙ δ = 8000 ∙ 0,5 = 4000 Av.

Dopolni n. c., je enaka vsoti magnetnih napetosti v posameznih odsekih: I ∙ ω = Hс ∙ lс + Hδ ∙ δ = 156 + 4000 = 4156 Av. I = (I ∙ ω) / ω = 4156/312 = 13,3 A.

Če je bil v prejšnjem primeru zahtevani magnetni pretok zagotovljen s tokom 0,5 A, potem je za magnetno vezje z zračno režo 0,5 cm potreben tok 13 A, da dobimo enak magnetni pretok. Iz tega je razvidno, da zračna reža, tudi nepomembna glede na dolžino magnetnega kroga, močno poveča zahtevani n. v. in tok tuljave.

4. Magnetni pretok transformatorja je izračunan na F = 72000 Ms. Potreben je izračun n.s.in magnetizacijski tok primarnega navitja z 800 obrati. V jedru transformatorja je reža δ = 0,2 mm. Dimenzije jedra transformatorja so prikazane na sl. 4. Prerez jedra S = 2 ∙ 3 ​​​​​​= 6 cm2 (transformatorji z jedri te oblike se imenujejo oklepni).

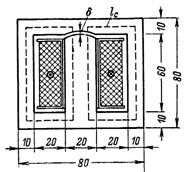
riž. 4.

Indukcija jedra in zračne reže B = F / S = 72000/6 = 12000 G.

Glede na krivuljo magnetizacije transformatorskega jekla za B = 12000 G določimo jakost: Hc = 5 A / cm.

Povprečna dolžina magnetne črte v jeklu je lс = 2 ∙ (6 + 3) = 18 cm.

Napetost v zračni reži Hδ = 0,8 ∙ B = 9600 A / cm.

Magnetna sila I ∙ ω = Hc ∙ lc + Hδ ∙ δ = 5 ∙ 18 + 9600 ∙ 0,02 = 90 + 192 = 282 Av; I = (I ∙ ω) / ω = 282/800 = 0,35 A.

V oklepnem jedru se magnetni tok razdeli na dva dela, ki sta zaprta vzdolž stranskih palic, katerih presek je S / 2, povprečna dolžina magnetne črte pa je lc. Zaradi tega je magnetno vezje popolnoma analogno magnetnemu vezju običajnega transformatorja s skupnim jedrom S in dolžino daljnovoda lc.

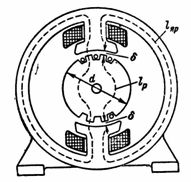
5. Magnetni pretok enosmernega stroja F = 1280000 Mks. Magnetno vezje vsebuje jarem iz litega jekla s povprečno dolžino magnetnega voda lа = 80 cm, rotor, sestavljen iz električnih jeklenih plošč s povprečno dolžino polja lр = 18 cm, in dve zračni reži δ 0,2 cm. = 8 ∙ 20 cm2; prerez rotorja in pola Sр = 12 ∙ 20 cm2... Izračunaj n. str in število obratov polne tuljave, če je največji magnetizacijski (vzburljivi) tok v njem 1 A (slika 5).

riž. 5.

Indukcija v jarmu in drogu Bя = Ф / Sя = 1280000/160 = 8000 G.

Napetost v jarmu in polu glede na krivuljo magnetizacije litega jekla pri Bя = 8000 G je enaka:

H = 2,8 A / cm.

Sila magnetizacije v odseku jarma HЯ ∙ la = 2,8 ∙ 80 = 224 Av.

Indukcija v rotorju, polu in zračni reži Br = Ф / Ср = 1280000/240 = 5333 G.

Napetost v rotorju iz jeklenih plošč pri Br = 5333 Gs Hrp = 0,9 A / cm,

in magnetna napetost odseka rotorja Hр ∙ lр = 0,9 ∙ 18 = 16,2 Av.

Napetost v zračni reži Hδ = 0,8 ∙ Bδ = 0,8 ∙ 5333 = 4266,4 A / cm.

Magnetna napetost v preseku zračne reže Hδ ∙ 2 ∙ δ = 4266,4 ∙ 2 ∙ 0,2 = 1706,56 A.

Dopolni n. c enaka vsoti magnetnih napetosti v posameznih odsekih: I ∙ ω = Hя ∙ la + Hр ∙ lр + Hδ ∙ 2 ∙ δ; I ∙ ω = 224 + 16,2 + 1706,56 = 1946,76 Av.

Število ovojev v dvopolnih tuljavah ω = (I ∙ ω) / I = 1946,76 / 1≈2000.