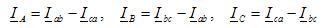Izračun trifaznih tokokrogov

Veriga trifazni izmenični tok sestoji iz trifaznega napajalnika, trifaznega porabnika in komunikacijskih vodnikov med njimi.

Simetrično trifazno napajanje je mogoče predstaviti kot tri enofazne vire, ki delujejo na isti frekvenci z enako napetostjo in s faznim kotom v času 120 °. Ti viri so lahko povezani v zvezdo ali trikot.

Pri povezovanju v zvezdo se pogojni začetek faz uporablja za povezavo treh linearnih vodnikov A, B, C, konci faz pa so združeni v eni točki, imenovani nevtralna točka vira energije (trifazni generator ali transformator). Na to točko je mogoče priključiti nevtralno žico N. Diagram zvezdne povezave vira energije je prikazan na sliki 1, a.

riž. 1. Priključni diagrami faz napajanja: a - zvezda; b - trikotnik

Napetost med linijo in nevtralnim vodnikom se imenuje faza, med vodniki pa linija (za več podrobnosti glejte tukaj – Linijska in fazna napetost).

V integrirana oblika vnosi izrazov za fazne napetosti so:

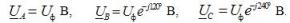
Ustrezne omrežne napetosti, ko so povezane v zvezdo:

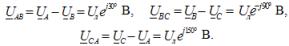
Tukaj je Uf modul fazne napetosti vira energije in Ul je modul omrežne napetosti. V simetričnem trifaznem sistemu, ko so izvorne faze povezane v zvezdo, obstaja razmerje med temi napetostmi:

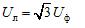
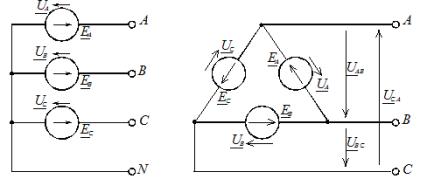
Ko so faze povezane s trikotnikom, so fazni napajalniki zaporedno povezani v zaprti zanki (slika 1, b).

Tri linearne žice A, B, C se izpeljejo iz točk združevanja virov med seboj, ki gredo do obremenitve. Iz slike 1, b je razvidno, da so izhodi faznih virov povezani z linearnimi žicami, zato so fazne napetosti, ko so faze vira povezane s trikotnikom, enake linearnim. V tem primeru ni nevtralne žice.

Obremenitev je mogoče priključiti na trifazno napajanje. Glede na velikost in naravo je lahko trifazna obremenitev simetrična in asimetrična.

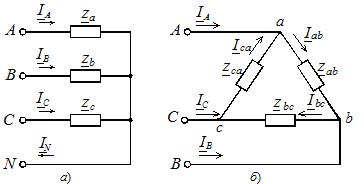
V primeru simetrične obremenitve so kompleksni upori treh faz enaki, in če so ti upori različni, potem je obremenitev neuravnotežena. Obremenitvene faze so lahko povezane med seboj v zvezdo ali trikot (slika 2), ne glede na shemo povezave vira.

riž. 2. Diagrami priključitve faz obremenitve

Zvezdna povezava je lahko z nevtralno žico ali brez (glej sliko 2, a). Odsotnost nevtralne žice odpravlja togo povezavo obremenitvene napetosti z napajalno napetostjo, v primeru asimetrične fazne obremenitve pa te napetosti niso enake druga drugi.Za njihovo razlikovanje smo se dogovorili, da bomo v črkovnih oznakah napajalnih napetosti in tokov uporabljali velike črke, v parametrih za obremenitev pa male črke.

Algoritem za analizo trifaznega vezja je odvisen od sheme priključka bremena, začetnih parametrov in namena izračuna.

Metoda dveh vozlišč se uporablja za določanje faznih napetosti pri neuravnoteženem zvezdno vezanem bremenu brez nevtralnega vodnika. Po tej metodi se izračun začne z določitvijo napetosti UN med nevtralnimi točkami napajanja in obremenitve, ki se imenuje napetost nevtralnega odstopanja:

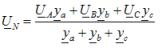
kjer ya, yb, yc - dovoljene vrednosti ustreznih faz obremenitve v kompleksni obliki

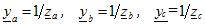
Napetosti med fazami neuravnotežene obremenitve se dobijo iz izrazov:

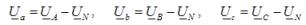
V posebnem primeru neuravnoteženosti obremenitve, ko v odsotnosti nevtralnega vodnika pride do kratkega stika v eni od faz obremenitve, je nevtralna prednapetost enaka fazni napetosti napajanja faze, v kateri je kratek stik prišlo.

Napetost na zaprti fazi bremena je enaka nič, na ostalih dveh pa je številčno enaka omrežni napetosti. Recimo, da na primer pride do kratkega stika v fazi B. Nevtralna prednapetost za ta primer je UN = UB. Nato fazne napetosti na bremenu:

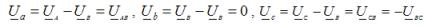
Fazni tokovi v obremenitvi so tudi tokovi linijskega prevodnika za katero koli vrsto obremenitve:

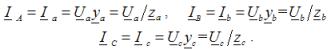
V nalogah pri izračunu trifaznih tokokrogov so upoštevane tri možnosti za povezovanje trifaznih porabnikov z zvezdo: povezava z nevtralno žico v prisotnosti porabnikov v treh fazah, povezava z nevtralno žico v odsotnosti porabnikov v eni faz in povezava brez nevtralne žice s kratko spojino v eni od bremenskih faz...

V prvi in ​​drugi različici se ustrezne fazne napetosti napajanja nahajajo na fazah obremenitve, fazni tokovi v obremenitvi pa so določeni z zgornjimi formulami.

V tretji različici napetost faz bremena ni enaka fazni napetosti napajanja in se določi z odvisnostmi

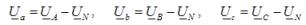
Tokovi v dveh fazah brez kratkega stika so določeni po Ohmovem zakonu, kot del deljenja fazne napetosti z impedanco zadevne faze. Tok kratkega stika se določi z enačbo, ki temelji na Prvi Kirchhoffov zakonsestavljen za nevtralno točko obremenitve.

Za zgornji primer kratkega stika faze B:

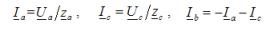
Za vsako vrsto bremena sta trifazna delovna in jalova moč enaka vsoti delovne oziroma jalove moči posameznih faz. Za določitev teh faznih moči lahko uporabite izraz

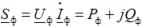
kjer je Uf,Azf kompleks napetosti in kompleks sklopljenih tokov v fazi obremenitve; Pf, Qf - aktivna in jalova moč v fazi obremenitve.

Trifazna delovna moč: P = Pa + Pb + Pc

Trifazna jalova moč: Q = Qa + Qb + Vc

Trifazna navidezna moč:

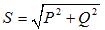
Ko so potrošniki povezani s trikotnikom, ima vezje obliko, prikazano na sliki 2, b. V tem načinu fazna povezava uravnoteženega napajanja ni pomembna.

Napetosti med napajalnimi vodi se zaznavajo na fazah bremena. Fazni tokovi v bremenu se določijo z uporabo Ohmov zakon za odsek vezjaAzf = Uf /zf, kjer je Uf - fazna napetost v obremenitvi (ki ustreza omrežni napetosti vira energije); zf je skupni upor ustrezne faze bremena.

Tokovi v linearnih vodnikih so določeni s faznimi tokovi na podlagi prvega Kirchhoffovega zakona za vsako vozlišče (točke a, b, c) vezja, prikazanega na sliki 2, b: