Teorija avtomatov, končni avtomati
Struktura, zasnova, načelo delovanja različnih strojev so v veliki meri odvisni od njegovega funkcionalnega namena. Razlikovati med tehnološkimi, transportnimi, računalniškimi, vojaškimi in drugimi stroji. Celotni avtomatski kompleksi, namenjeni izvajanju kompleksnih tehnoloških procesov, so široko uvedeni v različnih panogah. Avtomati so načrtovani in izdelani, ki opravljajo različne logične funkcije (logični stroji).
Teorija avtomatov — sekcija za kibernetiko, ki je nastal pod vplivom zahtev tehnologije digitalnih računalnikov in krmilnih strojev. Diskretni avtomati, ki jih preučuje teorija avtomatov, so abstraktni modeli realnih sistemov (tako tehničnih kot bioloških), ki obdelujejo diskretne (digitalne) informacije v diskretnih časovnih korakih.
Teorija avtomatov temelji na natančnih matematičnih konceptih, ki formalizirajo intuitivne ideje o delovanju (vedenju) avtomata in o njegovi strukturi (notranji strukturi).
Pri tem transformacijo informacij vedno razumemo kot operacijo, ki pretvori vhodna zaporedja, sestavljena iz črk vhodne abecede, v izhodna zaporedja, sestavljena iz črk izhodne abecede.
Široko se uporablja aparat matematične logike, algebre, teorije verjetnosti, kombinatorike in teorije grafov.
Težava s teorijo avtomatov v nekaterih njenih delih (strukturna teorija avtomatov) je naraščala iz teorije relejno-kontaktnih vezij, ki je začela nastajati v poznih tridesetih letih prejšnjega stoletja. vključno metode logične algebre.

V strukturni teoriji avtomatov se preučujejo različne vrste shem, ki opisujejo, kako je kompleksen avtomat ustvarjen iz enostavnejših komponent (elementov), ki so pravilno povezani v sistem.
Druga smer, imenovana abstraktna teorija avtomatov, preučuje vedenje avtomatov (to je naravo transformacije informacij, ki jih izvajajo), medtem ko abstrahira posebnosti njihove notranje strukture in je nastala v petdesetih letih prejšnjega stoletja.
V okviru abstraktne teorije avtomatov je vsebina pojmov "avtomat" in "stroj" v bistvu izčrpana s standardnim opisom transformacije informacij, ki jo izvaja avtomat. Takšna transformacija je lahko deterministična, lahko pa je tudi verjetnostne narave.
Najbolj raziskani so deterministični stroji (avtomati), ki vključujejo končne avtomate - glavni predmet študija v teoriji avtomatov.
Za končni avtomat je značilna omejena količina pomnilnika (število notranjih stanj) in je definiran s prehodno funkcijo.Z nekaj razumne idealizacije lahko vse sodobne matematične stroje in celo možgane z vidika njihovega delovanja obravnavamo kot končne avtomate.
Izrazi "zaporedni stroj", "Millyjev avtomat", "Moorov avtomat" se v literaturi (in ne enotno pri vseh avtorjih) uporabljajo kot sopomenke pojma "končni avtomat" ali za poudarjanje nekaterih značilnosti v prehodnih funkcijah končnega avtomata. avtomat.
Avtomat z neomejenim pomnilnikom je Turingov stroj, ki je sposoben izvesti (potencialno) kakršno koli učinkovito transformacijo informacij. Koncept "Turingov stroj" je nastal prej kot koncept "končnega stroja" in se v glavnem preučuje v teoriji algoritmov.
Teorija abstraktnih avtomatov je tesno povezana z dobro znanimi algebrskimi teorijami, na primer s teorijo polskupin. Z aplikativnega vidika so zanimivi rezultati, ki označujejo transformacijo informacij v avtomatu glede na velikost pomnilnika.
Tako je na primer pri problemih z eksperimenti na avtomatih (dela E. F. Moorea itd.), kjer se ena ali druga informacija o prehodnih funkcijah avtomata ali o zmogljivosti njegovega pomnilnika pridobi iz rezultatov poskusi.
Druga naloga je izračunati periode izhodnih zaporedij na podlagi razpoložljivih informacij o velikosti pomnilnika avtomata in periodah vhodnih zaporedij.
Zelo pomemben je razvoj metod za minimiziranje pomnilnika končnih avtomatov in preučevanje njihovega obnašanja v naključnih okoljih.
V teoriji abstraktnih avtomatov je problem sinteze naslednji.V nekem jasno formaliziranem jeziku so zapisani pogoji za obnašanje zasnovanega avtomata (za dogodek, ki je predstavljen v avtomatu). V tem primeru je treba razviti metode, ki glede na vsak zapisani pogoj:
1) ugotoviti, ali obstaja takšen stroj stanja, da informacije, ki jih transformira, izpolnjujejo ta pogoj;
2) če je odgovor pritrdilen, se konstruirajo prehodne funkcije takega končnega avtomata ali oceni velikost njegovega pomnilnika.
Rešitev naloge sinteze v takšni formulaciji predpostavlja predhodno ustvarjanje priročnega jezika za zapis delovnih pogojev avtomata s priročnimi algoritmi za prehod s snemanja na prehodne funkcije.
V strukturni teoriji avtomatov je problem sinteze sestavljen iz konstrukcije verige elementov danega tipa, ki realizira končni avtomat, ki ga dajejo njegove prehodne funkcije. V tem primeru običajno navedejo nek kriterij optimalnosti (na primer najmanjše število elementov) in poskušajo dobiti optimalno shemo.
Kot se je kasneje izkazalo, to pomeni, da so nekatere metode in koncepti, razviti prej v zvezi z relejnimi kontaktnimi vezji, uporabni za vezja druge vrste.
V povezavi z razvojem elektronskih tehnologij so najbolj razširjene sheme funkcionalnih elementov (logična omrežja). Poseben primer logičnih mrež so abstraktne nevronske mreže, katerih elemente imenujemo nevroni.
Razvitih je veliko metod sinteze, odvisno od vrste vezij in transformacije informacij, ki so jim namenjene (Sinteza relejnih naprav).
Poglej -Minimizacija kombinacijskih vezij, Carnotovi preslikavi, sinteza vezij
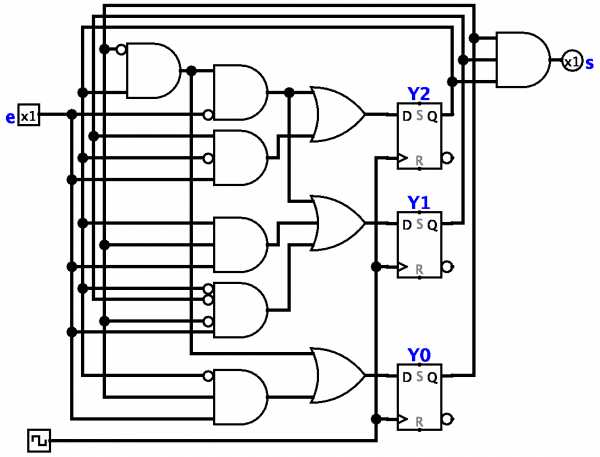
Končni stroj — matematični model krmilnega sistema s fiksno velikostjo pomnilnika (ki se med delovanjem ne more povečati).
Koncept končnega avtomata je matematična abstrakcija, ki označuje splošne značilnosti nabora krmilnih sistemov (na primer relejna naprava z več zankami). Vsi taki sistemi imajo skupne lastnosti, ki jih je naravno sprejeti kot definicijo končnega avtomata.
Vsak dokončan avtomat ima vhod, ki je izpostavljen zunanjim vplivom in notranjim elementom. Za vhodne in notranje elemente je določeno število ločenih stanj, ki jih lahko sprejmejo.
Sprememba stanja vhodnih in notranjih elementov se pojavi v diskretnih trenutkih časa, intervali med katerimi se imenujejo klopi. Notranje stanje (stanje notranjosti) na koncu traku je v celoti določeno z notranjim stanjem in stanjem vhoda na začetku traku.
Vse druge definicije končnega avtomata se lahko reducirajo na to karakteristiko, zlasti definicije, ki predpostavljajo, da ima končni avtomat izhod, ki je odvisen od notranjega stanja avtomata v danem trenutku.
V smislu takšne značilnosti je narava njegovih vhodov in notranjih stanj nepomembna za opis popolnega avtomata. Namesto vnosov in stanj lahko samo pogledate njihove številke v naključnem oštevilčevanju.
Stroj stanja bo nastavljen, če je določena odvisnost njegovega notranjega stanja od prejšnjega notranjega stanja in prejšnjega vhodnega stanja. Takšna naloga je lahko v obliki finalne mize.
Drug pogost način za definiranje popolnega avtomata je konstrukcija t.i prehodni diagrami. Vhodna stanja se pogosto imenujejo preprosto vhodi, notranja stanja pa preprosto stanja.
Končni avtomat je lahko model tako tehničnih naprav kot nekaterih bioloških sistemov. Avtomati prve vrste so na primer relejne naprave in različni elektronski računalniki, vklj. programabilni logični krmilniki.
V primeru relejne naprave vlogo vhodnih stanj igrajo kombinacije stanj občutljivih elementov relejne naprave (vsaka kombinacija takih stanj je "kompleksno stanje", za katero je značilna indikacija vseh občutljivih elementov relejne naprave). ta diskretna stanja, ki jih imajo v danem trenutku). Podobno kombinacije stanj vmesnih elementov relejne naprave delujejo kot notranja stanja.
Programabilni logični krmilnik (PLC) je primer relejne naprave, ki jo lahko imenujemo samostojni avtomat stanja.
Dejstvo je, da ko je program vnesen v PLC in krmilnik začne računati, ni izpostavljen zunanjim vplivom in je vsako naslednje stanje popolnoma odvisno od njegovega prejšnjega stanja. Predpostavimo lahko, da ima vhod enako stanje v vsakem taktu.
Nasprotno pa se vsak končni avtomat, ki ima edino možno vhodno stanje, naravno imenuje avtonomen, saj v tem primeru zunanje okolje ne nosi informacij, ki bi nadzorovale njegovo vedenje.
Poglej tudi:
Uporaba mikroprocesorskih sistemov v elektrotehniki na primeru uporabe PLC