Časovna konstanta električnega tokokroga — kaj je in kje se uporablja

Periodični procesi so neločljivo povezani z naravo: dnevu sledi noč, toplo sezono zamenja mraz itd. Obdobje teh dogodkov je skoraj konstantno in ga je zato mogoče strogo določiti. Še več, upravičeno trdimo, da kot primer navedeni periodični naravni procesi niso amortizirajoči, vsaj kar zadeva življenjsko dobo človeka.

Vendar v tehniki, predvsem v elektrotehniki in elektroniki, niso vsi procesi periodični in kontinuirani. Običajno se nekateri elektromagnetni procesi najprej povečajo in nato zmanjšajo. Pogosto je materija omejena le na fazo začetka nihanja, ki nima časa, da bi se zares pospešilo.

V elektrotehniki pogosto srečamo tako imenovane eksponentne prehode, katerih bistvo je v tem, da si sistem preprosto prizadeva doseči neko ravnotežno stanje, ki je na koncu videti kot stanje mirovanja. Tak prehod je lahko naraščajoč ali padajoč.

Zunanja sila najprej spravi dinamični sistem iz ravnovesja, nato pa ne prepreči naravne vrnitve tega sistema v prvotno stanje. Ta zadnja faza je tako imenovani prehodni proces, za katerega je značilno določeno trajanje. Poleg tega je tudi proces neuravnoteženosti sistema prehoden proces z značilnim trajanjem.

Tako ali drugače, časovno konstanto prehodnega procesa imenujemo njegova časovna karakteristika, ki določa čas, po katerem se bo določen parameter tega procesa spremenil za krat «e», to je, da se bo povečal ali zmanjšal za približno 2,718-krat. v primerjavi z začetnim stanjem.

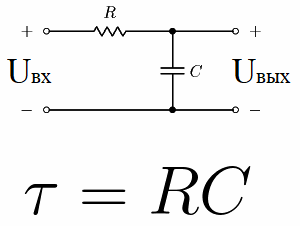
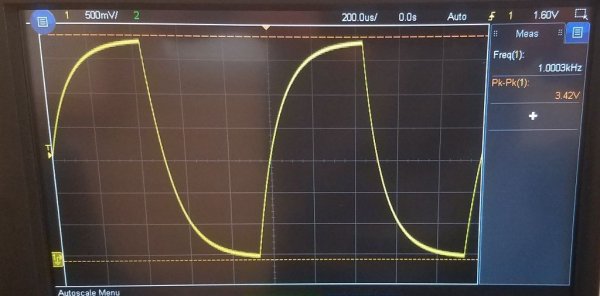
Razmislite na primer o električnem krogu, ki ga sestavljajo vir enosmerne napetosti, kondenzator in upor. Ta vrsta vezja, kjer je upor zaporedno povezan s kondenzatorjem, se imenuje RC integrirno vezje.

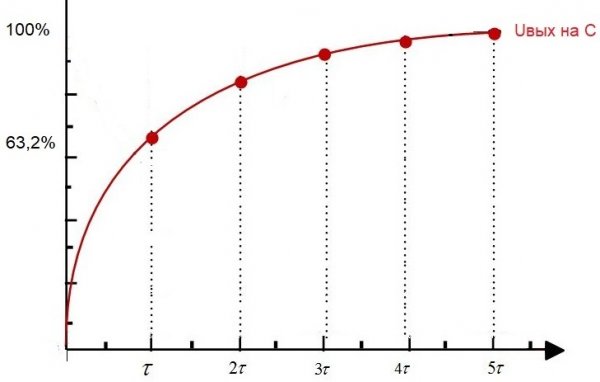
Če v začetnem trenutku napajate takšno vezje, to je, da nastavite konstantno napetost Uin na vhodu, potem bo Uout - napetost v kondenzatorju, začela eksponentno naraščati.

Po času t1 bo napetost kondenzatorja dosegla 63,2 % vhodne napetosti. Torej je časovni interval od začetnega trenutka do t1 časovna konstanta tega vezja RC.

Ta verižna konstanta se imenuje "tau", meri se v sekundah in je označena z ustrezno grško črko. Numerično je za vezje RC enako R * C, kjer je R v ohmih in C v faradih.

Integracijska vezja RC se uporabljajo v elektroniki kot nizkopasovni filtri, ko je treba višje frekvence odrezati (zadušiti) in prepustiti nižje frekvence.

V praksi mehanizem takšne filtracije temelji na naslednjem principu. Za izmenični tok kondenzator deluje kot kapacitivni upor, katerega vrednost je obratno sorazmerna s frekvenco, to pomeni, da višja kot je frekvenca, nižja bo reaktanca kondenzatorja v ohmih.

Torej, če izmenični tok teče skozi vezje RC, bo, tako kot na roki delilnika napetosti, padla določena napetost na kondenzatorju, sorazmerna z njegovo kapacitivnostjo pri frekvenci prehajajočega toka.

Če sta znani mejna frekvenca in amplituda vhodnega izmeničnega signala, potem projektantu ne bo težko izbrati takega kondenzatorja in upora v vezju RC, da bo minimalna (mejna) napetost (za mejna frekvenca — zgornja meja frekvence) pade na kondenzator, saj reaktanca vstopi v delilnik skupaj z uporom.

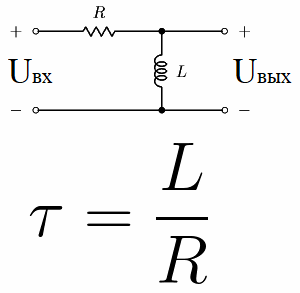
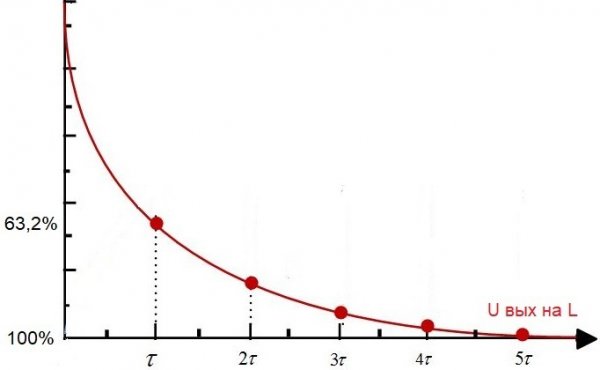
Zdaj razmislite o tako imenovanem diferencialnem vezju. To je vezje, sestavljeno iz zaporedno povezanih upora in induktorja, RL vezje. Njegova časovna konstanta je numerično enaka L / R, kjer je L induktivnost tuljave v henrijih, R pa upornost upora v ohmih.

Če se na takšno vezje uporabi konstantna napetost iz vira, se bo po določenem času tau napetost tuljave zmanjšala v primerjavi z U in za 63,2%, to je popolnoma v skladu z vrednostjo časovne konstante za to električno vezje. .

V tokokrogih AC (izmenični signali) se tokokrogi LR uporabljajo kot visokofrekvenčni filtri, ko je treba nizke frekvence odrezati (zadušiti) in frekvence nad (nad mejno frekvenco — spodnjo frekvenčno mejo) — izpustiti.Torej, višja kot je induktivnost tuljave, višja je frekvenca.

Kot v primeru zgoraj obravnavanega vezja RC, se tukaj uporablja načelo delilnika napetosti. Tok z višjo frekvenco, ki teče skozi vezje RL, bo povzročil večji padec napetosti na induktivnosti L, kot pri induktivnem uporu, ki je skupaj z uporom del delilnika napetosti. Naloga projektanta je izbrati takšna R in L, da dobimo minimalno (mejno) napetost tuljave točno na mejni frekvenci.