Topologije vezij – osnovni pojmi

Električni tokokrog je skupek naprav (elementov) in njihovih povezovalnih vodnikov, po katerih lahko teče električni tok. Vsi elementi električnih tokokrogov so skupni v pasivnem in aktivnem.

Aktivni elementi pretvarjajo različne vrste energije (mehansko, kemično, svetlobno itd.) v električno energijo. V pasivnih napravah se električna energija pretvarja v druge vrste energije. Aktivne elemente imenujemo viri, pasivne porabnike ali sprejemnike.

V teoriji vezij se obravnavajo idealizirani modeli električnih elementov. Tako je opis elementov čim bolj preprost. Kompleksnejši, resnični elementi so modelirani iz nabora idealiziranih elementov.

Glavni pasivni elementi električnih tokokrogov so upor (uporovni element), induktor (induktivni element) in kondenzator (kapacitivni element). Elementi so nameščeni v električnem tokokrogu za ustvarjanje napetosti in toka določene vrednosti in oblike (glej — Električni krog in njegovi elementi).

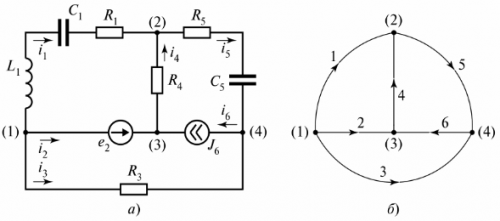
Električni krog je sestavljen iz vej in vozlišč. Podružnica — to je odsek električnega tokokroga (kroga), skozi katerega teče isti tok. Vozel — povezava treh ali več vej. Na električni shemi je vozlišče označeno s piko (slika 1).

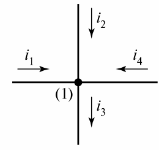
riž. 1. Definirajte vozlišče v diagramu

Po potrebi so vozlišča diagrama oštevilčena od leve proti desni od zgoraj navzdol.

Na sl. 2 prikazuje uporovno-kapacitivno vejo, v kateri teče tok iC.

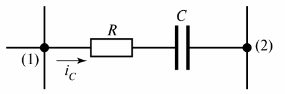
riž. 2. Uporovno-kapacitivna veja

Lahko podamo še eno definicijo veje - to je odsek vezja med dvema sosednjima vozliščema (vozlišči (1) in (2) na sliki 2).

Veriga Ali obstaja kakšna zaprta pot v električnem tokokrogu. Vezje je mogoče zapreti s poljubnimi vejami, vključno s pogojnimi vejami, katerih upor je enak neskončnosti.

Na sl. 3 prikazuje razvejano električno vezje, ki je sestavljeno iz treh vej.

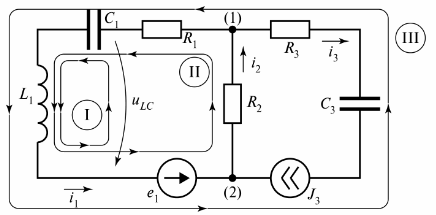
riž. 3. Električni tokokrog z dvema vezjema

Diagram prikazuje tri vezja, vezje I pa je zaprto z vejo neskončnega upora. Ta veja je označena kot napetost tiLC.

Za vezje na sl. 3 je mogoče sestaviti veliko zank, ki so zaprte z realnimi ali pogojnimi vejami, vendar se za izračun električnega šuma uporablja koncept "neodvisne zanke". Število neodvisnih zank vezja je vedno nastavljeno kot najmanjše, potrebno za izračun.

Neodvisna vezja so vedno zaprta, vendar veje, katerih upor ni enak neskončnosti, in vsako neodvisno vezje vključuje vsaj eno vejo, ki ni vključena v druga vezja. Za zapletena električna vezja lahko določite število neodvisnih vezij z uporabo diagrama vezja.

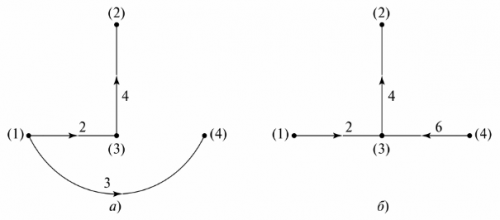
Na shemi vezja se imenuje pogojna predstavitev vezja, v kateri je vsaka veja nadomeščena z odsekom črte. Postavke v poslovalnicah niso prikazane. Na sl. 4 prikazuje razvejno vezje in njegov diagram.

riž. 4. Razvejano električno vezje: a — shema vezja, b — shema

Če želite narediti diagram diagrama, morate povezati vozlišča z vejami, ne da bi na njih določili elemente. Veje so oštevilčene, smeri tokov na njih pa so označene s puščicami. Sam graf nima fizikalnega pomena, lahko pa ga uporabimo za določitev števila in vrste neodvisnih kontur. V ta namen je pripravljeno »grafično drevo«.

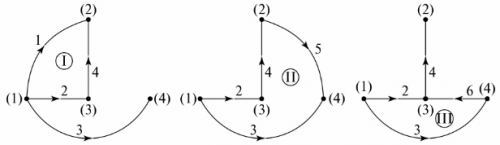
Grafično drevo Predstavlja graf vezja, katerega vozlišča so povezana z vejami na tak način, da ne pride do zaprte zanke. Za prikaz grafičnega drevesa je lahko več možnosti. Na sl. 5 prikazuje dve možni možnosti za vezje s sl. 4.

riž. 5. Grafično drevo sheme

Število manjkajočih vej v drevesu grafa je enako številu neodvisnih zank vezja. V primeru so to tri veje, tri neodvisne zanke. Konfiguracijo neodvisnih zank je mogoče doseči z zaporedno povezavo vozlišč drevesa grafa z vejami, ki niso navedene v drevesu grafa. Na primer, za grafično drevo na sl. 5, neodvisne konture pa so prikazane na sl. 6.

riž. 6. Določanje neodvisnih kontur skozi grafično drevo

Izbira možnosti za konfiguracijo neodvisnih vezij za izračun vezja se izvede med analizo vezja. Izbrati morate takšne konture, da bo izračun čim preprostejši, tj. število odvisnih enačb v sistemu je minimalno.

Topološke enačbe vzpostavljajo razmerje med napetostmi in tokovi v vezju, število in vrsta enačb pa nista odvisna od tega, kateri elementi so vključeni v veje. Topološke enačbe vključujejo enačbe, sestavljene iz po Kirchhoffovih zakonih.