Nerazvejana in razvejana linearna električna vezja z enim napajanjem
Če je veliko število pasivnih elementov skupaj z virom e. itd. c) tvorijo električni tokokrog, njihova medsebojna povezava se lahko izvede na različne načine. Obstajajo naslednje tipične sheme za takšne povezave.
Serijska povezava elementov To je najenostavnejša povezava. S to povezavo teče enak tok v vseh elementih vezja. V skladu s to shemo je mogoče povezati bodisi vse pasivne elemente vezja, nato pa bo vezje enokrožno nerazvejano (slika 1., a) ali pa je lahko le del elementov vezja z več vezji povezan.
Če je zaporedno povezanih n elementov, v katerih teče isti tok I, bo napetost na sponkah vezja enaka vsoti padcev napetosti v zaporedno vezanih n elementih, tj.
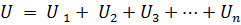
ali:
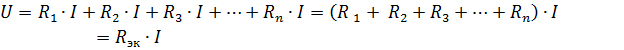
kjer je Rek upor ekvivalentnega vezja.
Zato je ekvivalentna upornost zaporedno vezanih pasivnih elementov enaka vsoti upornosti teh elementov... Električna shema (sl.1, a) je mogoče predstaviti ekvivalentno vezje (slika 1, b), sestavljeno iz enega elementa z enakovrednim uporom Rek
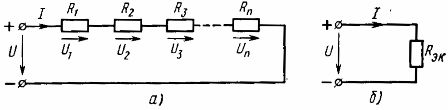
riž. 1. Shema serijske povezave linearnih elementov (a) in njena enakovredna shema (b)
Pri izračunu vezja z zaporedno vezanimi elementi pri določeni napetosti vira energije in upornosti elementov se tok v vezju izračuna po Ohmovem zakonu:
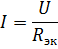
Padec napetosti na k-tem elementu
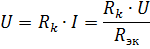
ni odvisna le od upora tega elementa, temveč tudi od ekvivalentnega upora Rek, to je od upora drugih elementov vezja. To je pomembna pomanjkljivost serijske povezave elementov. V omejevalnem primeru, ko upornost katerega koli elementa vezja postane enaka neskončnosti (odprto vezje), tok v vseh elementih vezja postane nič.
Ker je pri zaporedni povezavi tok v vseh elementih vezja enak, je razmerje padca napetosti v elementih enako razmerju uporov teh elementov:
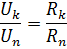
Vzporedna povezava elementov - to je povezava, pri kateri se na vse elemente vezja uporablja enaka napetost. V skladu s shemo vzporedne povezave se lahko povežejo vsi pasivni elementi vezja (slika 2, a) ali le del njih. Vsak vzporedno povezan element tvori ločeno vejo. Zato je vezje z vzporedno povezavo elementov, prikazano na sl. 2, a, čeprav gre za preprosto vezje (ker vsebuje samo dve vozlišči), je hkrati razvejano.
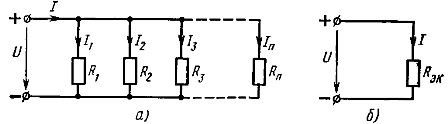
riž. 2. Shema vzporedne povezave linearnih elementov (a) in njena enakovredna shema (b)
V vsaki vzporedni veji je tok
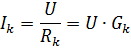
kjer je Gk prevodnost k-te veje.
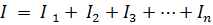
oz
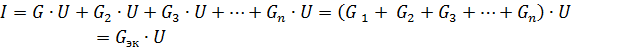
kjer je Gec ekvivalentna prevodnost vezja.
Zato je pri vzporedni vezavi pasivnih elementov njihova ekvivalentna prevodnost enaka vsoti prevodnosti teh elementov... Ekvivalentna prevodnost je vedno večja od prevodnosti kateregakoli dela vzporednih vej. Ekvivalentna prevodnost GEK ustreza ekvivalentnemu uporu Rek = 1 / Gek.
Potem je ekvivalentno vezje, prikazano na sl. 2, a, bo imela obliko, prikazano na sl. 2, b Tok v nerazvejanem delu vezja z vzporedno povezavo elementov lahko določimo iz tega vezja po Ohmovem zakonu:
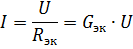
Torej, če je napajalna napetost konstantna, se s povečanjem števila vzporedno povezanih elementov (kar vodi do povečanja ekvivalentne prevodnosti) poveča tok v nerazvejanem delu vezja (napajalni tok).
Iz formule
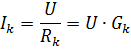
razvidno je, da je tok v vsaki veji odvisen samo od prevodnosti te veje in ni odvisen od prevodnosti drugih vej. Neodvisnost vzporednih vej drug od drugega je pomembna prednost vzporedne povezave pasivnih elementov. V industrijskih inštalacijah se v večini primerov uporablja vzporedna povezava električnih sprejemnikov. Najbolj očiten primer je vključitev električnih svetilk za razsvetljavo.
Ker pri vzporedni povezavi na vse elemente deluje enaka napetost in je tok v vsaki veji sorazmeren s prevodnostjo te veje, je razmerje tokov v vzporednih vejah enako razmerju prevodnosti teh vej ali obratno sorazmerno glede na razmerje njihovih uporov:
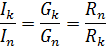
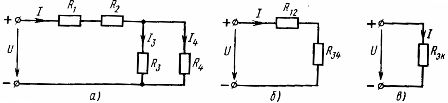
Mešana vezava elementov je kombinacija zaporednih in vzporednih povezav. Takšna veriga ima lahko različno število vozlišč in vej. Primer mešane povezave je prikazan na diagramu (slika 3, a)
riž. 3. Shema mešane povezave linearnih elementov (a) in njene enakovredne sheme (b, c).
Za izračun takšnega vezja je treba zaporedno določiti ekvivalentne upore za tiste dele vezja, ki so samo zaporedno ali samo vzporedno povezani. V obravnavanem vezju je serijsko vezava elementov z uporoma R1 in R2 ter vzporedna vezava elementov z uporoma R3 in R4. Z uporabo predhodno pridobljenih razmerij med parametri elementov vezja z njihovo zaporedno in vzporedno vezavo lahko realno električno vezje zaporedno nadomestimo z enakovrednimi vezji.
Ekvivalentna upornost zaporedno povezanih elementov
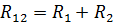
Ekvivalentna upornost vzporedno povezanih elementov R3 in R4
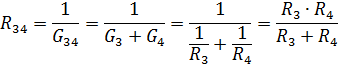
Enakovredno vezje z upornostmi elementov R12 in R34 je prikazano na sl. 3, b. Za to zaporedno povezavo R12 in R34 je enakovreden upor
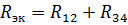
in ustrezno ekvivalentno vezje je prikazano na sl. 2, b. Poiščimo tok v tem vezju:
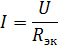
To sta napajalni tok in tok v elementih R1 in R2 realnega vezja.Za izračun tokov I3 in I4 določite napetost v odseku vezja z uporom R34 (slika 3, b):
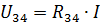
Potem lahko tokove I3 in I4 najdemo po Ohmovem zakonu:
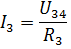
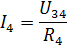
Na podoben način lahko izračunate številna druga električna vezja z mešano povezavo pasivnih elementov.
Za kompleksna vezja z velikim številom vezij in virov e. itd. c) takšne enakovredne pretvorbe ni mogoče vedno izvesti. Izračunajo se z drugimi metodami.