Napetostna resonanca

Če je izmenični tokokrog povezan zaporedno induktor in kondenzator, potem na svoj način vplivajo na generator, ki napaja tokokrog in fazne povezave med tokom in napetostjo.

Induktor povzroči fazni zamik, kjer tok zaostaja za napetostjo za četrtino periode, medtem ko kondenzator, nasprotno, povzroči, da napetost v vezju zaostaja za tokom za četrtino periode. Tako je učinek induktivnega upora na fazni premik med tokom in napetostjo v vezju nasproten učinku kapacitivnega upora.

To vodi do dejstva, da je skupni fazni premik med tokom in napetostjo v vezju odvisen od razmerja vrednosti induktivnega in kapacitivnega upora.

Če je vrednost kapacitivnega upora vezja večja od induktivne, potem je vezje po naravi kapacitivno, to pomeni, da napetost zaostaja za tokom v fazi. Če je, nasprotno, induktivni upor vezja večji od kapacitivnega, potem napetost vodi tok in je zato vezje induktivno.

Skupna reaktanca Xtot vezja, ki ga obravnavamo, je določena z dodajanjem induktivnega upora tuljave XL in kapacitivnega upora kondenzatorja XC.

Ker pa je delovanje teh uporov v tokokrogu nasprotno, je enemu od njih, in sicer Xc, dodeljen znak minus, skupna reaktanca pa je določena s formulo:

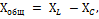
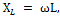
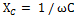
Uporabi za to vezje Ohmov zakon, dobimo:

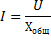
To formulo je mogoče preoblikovati na naslednji način:

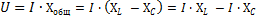
V dobljeni enačbi sta AzxL — efektivna vrednost komponente celotne napetosti vezja, ki bo premagala induktivni upor vezja, in AzNSC — efektivna vrednost komponente celotne napetosti vezja, ki bo premagajte kapacitivni upor.

Tako lahko celotno napetost vezja, sestavljenega iz serijske povezave tuljave in kondenzatorja, obravnavamo kot sestavljeno iz dveh členov, katerih vrednosti so odvisne od vrednosti induktivnega in kapacitivnega upora vezje.

Verjeli smo, da takšno vezje nima aktivnega upora. Vendar pa v primerih, ko aktivni upor vezja ni več tako majhen, da bi bil zanemarljiv, se skupni upor vezja določi z naslednjo formulo:

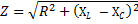
kjer je R skupni aktivni upor vezja, XL -NSC — njegova skupna reaktanca. Če se premaknemo na formulo Ohmovega zakona, imamo pravico napisati:

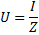
Resonanca izmenične napetosti

Induktivni in kapacitivni upori, vezani zaporedno, povzročijo manjši fazni premik med tokom in napetostjo v izmeničnem tokokrogu, kot če bi bili v tokokrog vključeni ločeno.

Z drugimi besedami, zaradi hkratnega delovanja teh dveh reakcij različne narave v tokokrogu pride do kompenzacije (medsebojnega uničenja) faznega premika.

Popolna odškodnina, tj. popolna odprava faznega zamika med tokom in napetostjo v takem vezju se bo zgodila, ko bo induktivni upor enak kapacitivnemu uporu vezja, to je, ko je XL = XC ali, kar je enako, ko je ωL = 1 / ωC.

V tem primeru se bo vezje obnašalo kot čisto aktivni upor, to je, kot da nima niti tuljave niti kondenzatorja. Vrednost tega upora je določena z vsoto aktivnih uporov tuljave in povezovalnih žic. Pri katerem efektivni tok v vezju bo največji in je določen s formulo Ohmovega zakona I = U / R, kjer je Z zdaj nadomeščen z R.

Hkrati bosta napetosti, ki delujeta na tuljavi UL = AzxL in na kondenzatorju Uc = AzNSCC, enaki in čim večji. Pri nizki aktivni upornosti vezja lahko te napetosti večkrat presežejo skupno napetost U sponk vezja. Ta zanimiv pojav se v elektrotehniki imenuje napetostna resonanca.

Na sl. 1 prikazuje krivulje napetosti, tokov in moči pri resonančnih napetostih v vezju.

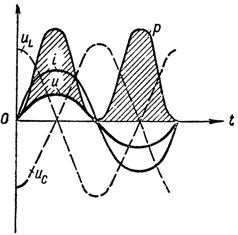
Graf napetostnega toka in moči pri napetostni resonanci

Upoštevati je treba, da sta upora XL in C spremenljivki, ki sta odvisni od frekvence toka in je vredno vsaj rahlo spremeniti njegovo frekvenco, na primer povečati, saj se bo povečal XL = ωL in XSC = = 1 / ωC se bo zmanjšal in tako bo napetostna resonanca v tokokrogu takoj motena, medtem ko se bo poleg aktivnega upora v tokokrogu pojavila tudi reaktanca. Enako se bo zgodilo, če spremenite vrednost induktivnosti ali kapacitivnosti vezja.

Z napetostno resonanco bo moč tokovnega vira porabljena samo za premagovanje aktivnega upora vezja, to je za ogrevanje žic.

Pravzaprav v vezju z eno induktivno tuljavo prihaja do energijskih nihanj, tj. periodični prenos energije od generatorja do magnetno polje tuljave. V krogu s kondenzatorjem se zgodi isto, vendar zaradi energije električnega polja kondenzatorja. V vezju s kondenzatorjem in induktorjem pri napetostni resonanci (ХL = XС) energija, ki jo vezje shrani, periodično prehaja iz tuljave v kondenzator in obratno, in le poraba energije, ki je potrebna za premagovanje aktivnega upora tokokrog pade na delež vira toka. Zato izmenjava energije poteka med kondenzatorjem in tuljavo skoraj brez sodelovanja generatorja.

Treba je samo prekiniti napetostno resonanco po vrednosti, kako postane energija magnetnega polja tuljave drugačna od energije električnega polja kondenzatorja in v procesu izmenjave energije med tema poljema bo presežek energije pojavi, ki bo občasno pritekel iz vira v tokokrogu, nato pa ga vrnil nazaj v tokokrog.

Ta pojav je zelo podoben tistemu, kar se dogaja v urnem mehanizmu. Urno nihalo bi lahko neprekinjeno nihalo brez pomoči vzmeti (ali uteži v urah), če ne bi bilo sil trenja, ki upočasnjujejo njegovo gibanje.

Vzmet s tem, da v pravem trenutku prenese del svoje energije na nihalo, mu pomaga premagati sile trenja in tako doseže kontinuiteto nihanja.

Podobno v električnem tokokrogu, ko se v njem pojavi resonanca, tokovni vir porabi svojo energijo samo za premagovanje aktivnega upora tokokroga in tako pomaga pri nihajnem procesu v njem.

Tako pridemo do zaključka, da krog izmeničnega toka, sestavljen iz generatorja in zaporedno vezanih induktorja in kondenzatorja, pod določenimi pogoji XL = XС postane nihajni sistem... To vezje so poimenovali nihajni krog.

Iz enačbe XL = XС je mogoče določiti vrednosti frekvence generatorja, pri kateri pride do pojava napetostne resonance:

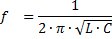
Pomen kapacitivnosti in induktivnosti vezja, kjer pride do napetostne resonance:

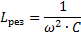
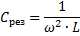
Tako lahko s spremembo katere koli od teh treh količin (eres, L in C) povzročimo napetostno resonanco v vezju, to je, da vezje spremenimo v nihajno vezje.

Primer uporabne uporabe napetostne resonance: Vhodno vezje sprejemnika je prilagojeno s spremenljivim kondenzatorjem (ali variometrom) tako, da se v njem pojavi napetostna resonanca. To doseže veliko povečanje napetosti tuljave, potrebne za normalno delovanje sprejemnika, v primerjavi z napetostjo tokokroga, ki jo ustvari antena.

Poleg koristne uporabe pojava napetostne resonance v elektrotehniki so pogosto primeri, ko je napetostna resonanca škodljiva.Veliko povečanje napetosti v posameznih odsekih tokokroga (na tuljavi ali na kondenzatorju) v primerjavi z napetostjo generatorja lahko povzroči poškodbe posameznih delov in merilnih naprav.