Kaj je električna oskrba?

Sodobni človek se v vsakdanjem življenju in pri delu nenehno srečuje z elektriko, uporablja naprave, ki porabljajo električni tok, in naprave, ki ga proizvajajo. Pri delu z njimi morate vedno upoštevati njihove zmogljivosti, ki so del tehničnih lastnosti.

Eden glavnih indikatorjev katere koli električne naprave je taka fizikalna količina, kot je električna energija ... Običajno imenujemo intenzivnost ali hitrost proizvodnje, prenosa ali pretvorbe električne energije v druge vrste energije, na primer toploto, svetlobo, mehanski.

Prevoz ali prenos velike električne energije za industrijske namene se izvaja po visokonapetostni daljnovodi.

Preoblikovanje električna energija se izvaja na transformatorskih postajah.

Poraba električne energije se pojavlja v gospodinjskih in industrijskih napravah za različne namene. Ena od njihovih pogostih vrst je žarnice z žarilno nitko različnih moči.

Električna moč generatorjev, daljnovodov in porabnikov v tokokrogih DC in AC ima enak fizikalni pomen, ki se hkrati izraža v različnih razmerjih glede na obliko sestavljenih signalov. Opredeliti splošne vzorce, pojme trenutnih vrednosti... Ponovno poudarjajo odvisnost hitrosti transformacije elektrike od časa.

Določanje trenutne električne moči

V teoretični elektrotehniki se za izpeljavo osnovnih razmerij med tokom, napetostjo in močjo uporabljajo njihove slike v obliki trenutnih vrednosti, ki so določene v določenem trenutku.

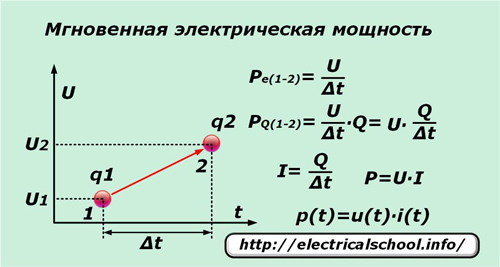
Če se v zelo kratkem času ∆t en elementarni naboj q pod vplivom napetosti U premakne iz točke «1» v točko «2», potem opravi delo, ki je enako potencialni razliki med tema točkama. Če ga delimo s časovnim intervalom ∆t, dobimo izraz za trenutno moč na enoto naboja Pe (1-2).

Ker se pod delovanjem uporabljene napetosti ne premika le posamezen naboj, temveč tudi vsi sosednji, ki so pod vplivom te sile, katerih število je priročno predstavljeno s številom Q, potem je trenutna vrednost moči PQ (1-2) lahko zapišemo zanje.

Po izvedbi preprostih transformacij dobimo izraz za moč P in odvisnost njene trenutne vrednosti p (t) od komponent produkta trenutnega toka i (t) in napetosti u (t).

Določanje konstantne električne moči

V DC tokokrogi velikost padca napetosti v odseku vezja in tok, ki teče skozi to, se ne spremeni in ostane stabilen, enak trenutnim vrednostim.Zato je moč v tem vezju mogoče določiti tako, da te vrednosti pomnožimo ali popolno delo A delimo z obdobjem njegovega izvajanja, kot je prikazano na pojasnjevalni sliki.

Določanje električne moči izmeničnega toka

Zakoni sinusoidnega spreminjanja tokov in napetosti, ki se prenašajo po električnih omrežjih, vplivajo na izražanje moči v takih vezjih. Tu pride v poštev navidezna moč, ki je opisana s trikotnikom moči in je sestavljena iz aktivne in jalove komponente.

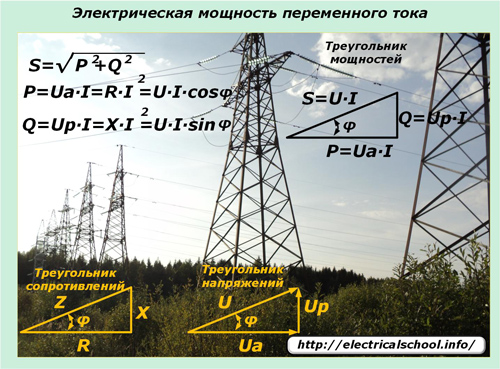
Sinusoidni električni tok pri prehodu skozi daljnovode z mešanimi vrstami obremenitev v vseh odsekih ne spremeni oblike svojega harmonika, padec napetosti pri reaktivnih obremenitvah pa se premakne v fazi v določeni smeri. Izrazi vrednosti momenta pomagajo razumeti učinek uporabljenih obremenitev na spremembo moči v vezju in njegovo smer.

Hkrati bodite pozorni na dejstvo, da sta smer toka toka od generatorja do potrošnika in prenesena moč skozi ustvarjeno vezje popolnoma različni stvari, ki v nekaterih primerih morda ne le ne sovpadata, ampak tudi usmerjeni v nasprotnih smereh.

Upoštevajte ta razmerja v njihovi idealni, čisti manifestaciji za različne vrste obremenitev:

• aktiven;

• kapacitivni;

• induktivni.

Moč aktivnega bremena

Predpostavili bomo, da generator proizvaja idealno sinusno napetost u, ki se nanaša na čisto aktivni upor vezja. Ampermeter A in voltmeter V merita tok I in napetost U vsakič, ko t.

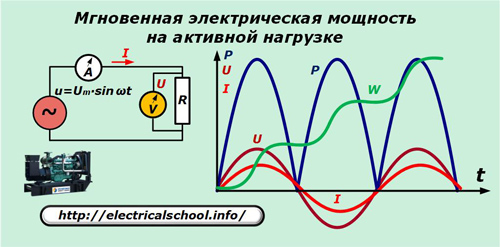
Graf kaže, da se sinusoide toka in padca napetosti na aktivnem uporu ujemata po frekvenci in fazi, kar povzroči enaka nihanja. Sila, izražena z njunim produktom, niha z dvakratno frekvenco in vedno ostane pozitivna.

p = u ∙ i = Um ∙ sinωt ∙ Um / R ∙ sinωt = Um2/ R ∙ sin2ωt = Um2/ 2R ∙ (1-cos2ωt).

Če gremo k izrazu delovna napetost, potem dobimo: p = P ∙ (1-cos2ωt).

Nato bomo integrirali moč v obdobju enega nihanja T in opazili bomo, da se dobiček energije ∆W v tem intervalu povečuje. Sčasoma upor še naprej porablja nove porcije električne energije, kot je prikazano na grafu.

Pri reaktivnih obremenitvah so značilnosti porabe energije drugačne, imajo drugačno obliko.

Kapacitivno odvajanje moči

V električnem tokokrogu generatorja zamenjajte uporovni element s kondenzatorjem kapacitivnosti C.

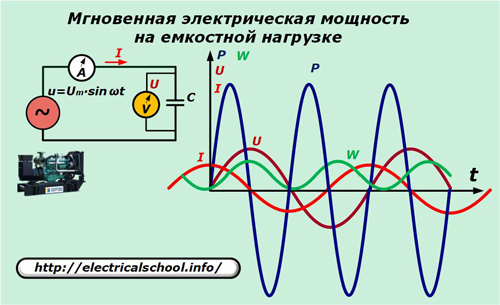
Razmerje med tokom in padcem napetosti v kapacitivnosti je izraženo z razmerjem: I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt.

Vrednosti trenutnih izrazov toka pomnožimo z napetostjo in dobimo vrednost moči, ki jo porabi kapacitivno breme.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2∙ sinωt ∙ cosωt = Um2/ (2X° C) ∙ sin2ωt = U2/ (2X° C) ∙ sin2ωt.

Tukaj lahko vidite, da moč niha okoli ničle pri dvakratni frekvenci uporabljene napetosti. Njegova skupna vrednost za harmonično obdobje, kot tudi dobiček energije, je nič.

To pomeni, da se energija giblje po sklenjenem krogu kroga v obe smeri, vendar ne deluje.To dejstvo je razloženo z dejstvom, da ko se napetost vira poveča v absolutni vrednosti, je moč pozitivna, tok energije skozi vezje pa je usmerjen v posodo, kjer se energija kopiči.

Ko napetost preide v padajoči harmonski del, se energija vrne iz kondenzatorja v vezje k viru. V nobenem procesu ni opravljeno nobeno koristno delo.

Disipacija moči pri induktivni obremenitvi

Zdaj v napajalnem krogu zamenjajte kondenzator z induktivnostjo L.

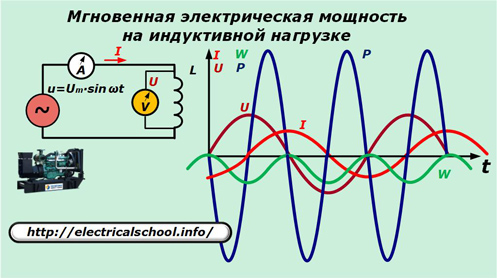
Tukaj je tok skozi induktivnost izražen z razmerjem:

I = 1 / L∫udt = -Um / ωL ∙ cos ωt.

Potem dobimo

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ sinωt ∙ cosωt = -Um2/ (2ХL) ∙ sin2ωt = -U2/ (2ХL) ∙ sin2ωt.

Dobljeni izrazi nam omogočajo, da vidimo naravo spremembe smeri moči in povečanja energije na induktivnosti, ki izvaja enaka nihanja, ki so neuporabna za opravljanje dela, kot na kapacitivnosti.

Moč, sproščena v reaktivnih obremenitvah, se imenuje reaktivna komponenta. V idealnih razmerah, ko povezovalne žice nimajo aktivnega upora, se zdi neškodljivo in ne povzroča nobene škode. Toda v realnih močnostnih pogojih periodični prehodi in nihanja jalove moči povzročijo segrevanje vseh aktivnih elementov, vključno s priključnimi vodniki, za kar se porabi nekaj energije in zmanjša vrednost uporabljene polne moči vira.

Glavna razlika med reaktivno komponento moči je, da sploh ne opravlja koristnega dela, ampak vodi do izgub električne energije in prekomernih obremenitev opreme, ki so še posebej nevarne v kritičnih situacijah.

Iz teh razlogov je za odpravo vpliva jalove moči, npr tehnični sistemi za njeno kompenzacijo.

Porazdelitev moči pri mešani obremenitvi

Kot primer uporabimo obremenitev generatorja z aktivno kapacitivno karakteristiko.

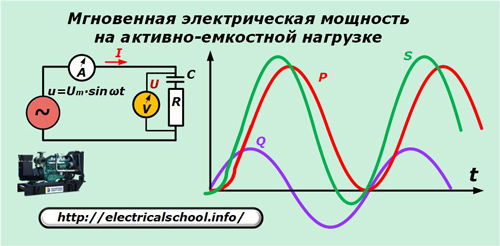
Za poenostavitev slike sinusoide tokov in napetosti v danem grafu niso prikazane, vendar je treba upoštevati, da pri aktivno-kapacitivni naravi obremenitve trenutni vektor vodi napetost.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Im ∙ sin (ωt + φ).

Po transformacijah dobimo: p = P ∙ (1- cos 2ωt) + Q ∙ sin2ωt.

Ta dva izraza v zadnjem izrazu sta aktivna in jalova komponenta trenutne navidezne moči. Samo prvi od teh opravlja koristno delo.

Orodja za merjenje moči

Za analizo porabe električne energije in izračun zanjo se uporabljajo merilne naprave, ki se že dolgo imenujejo «Števci»… Njihovo delo temelji na merjenju efektivnih vrednosti toka in napetosti in njihovem avtomatskem množenju z izhodnimi informacijami.

Števci prikazujejo porabo energije tako, da štejejo čas delovanja električnih naprav inkrementalno od trenutka vklopa števca pod obremenitvijo.

Za merjenje aktivne komponente moči v AC tokokrogih, vatmetri, in reaktivni - varmetri. Imajo različne oznake enot:

• vat (W, W);

• var (var, var, var).

Za določitev skupne porabe energije je potrebno izračunati njeno vrednost s formulo trikotnika moči na podlagi odčitkov vatmetra in varmetra. Izražen je v lastnih enotah - volt-amperih.

Sprejete oznake enot vsake pomagajo električarjem, da ocenijo ne le njegovo vrednost, temveč tudi naravo komponente moči.